Visual Proofs

My Differential equation prof while making use of Pythagoras theorem in an equation drew these cute little visual proofs on the board:

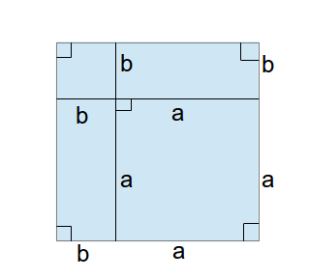
(a + b)² = a² + 2 ab + b²

(a + b)² = c² + 4 (ab/2)

c² = a² + b²

I had seen a couple of visual proofs sometime back, but din’t follow it up. Yesterday I spent some time googling them up and I’m truly amazed! There’s a whole bunch of them, and some interesting ones can be found in this Quora thread, Bill the lizard’s blog and mathoverflow. The theme of the ones I’ve shared is calculating areas of rectangles and composite shapes made from rectangles.

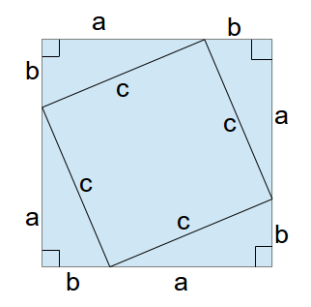
Here are 2 more ‘proofs without words’ for you to admire! Sorry about the not so accurate drawing on my part, hope you get the idea!

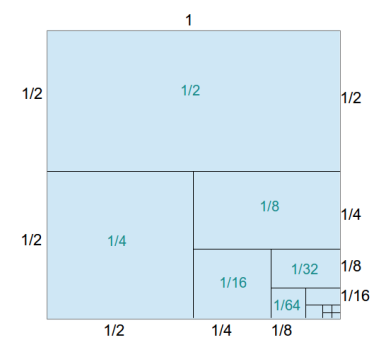
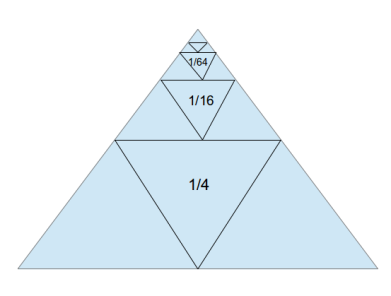
1/2 + 1/4 + 1/16 + 1/32 + 1/64 + … = 1

 1/4 + 1/16 + 1/64 + … = 1/3

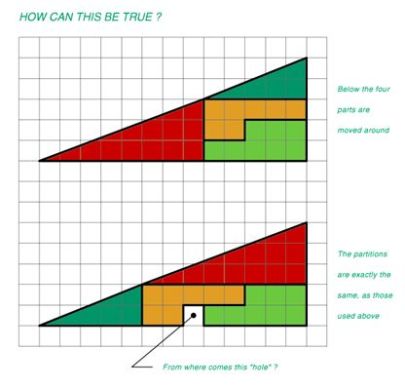
These also make up for some good puzzles and/or illusions. Check this one for example:

Insane! Here’s a proof (scroll down) of exactly how wrong this is. Knock yourself out! 🙂